What's New
 | Hsu-Chun successfully defended her thesis. Congrats Dr. Tsai! |
 | Yujun successfully defends her thesis. Congrats Dr. Tao! |
 | Erika wins 2024 Van Dyke Award. Congratulations Erika! |
 | Jinzhe wins Reid Award. Congratulations Jinzhe! |
 | We're hiring GPU programmers! |
 | Erika wins 2024 IQB Inclusive Leadership Award! |
 | Darrin's review AFE Methods review is out and featured on the cover (THANKS YUJUN!) |
 | Yujun makes the cover of ACS Environmental Au! |
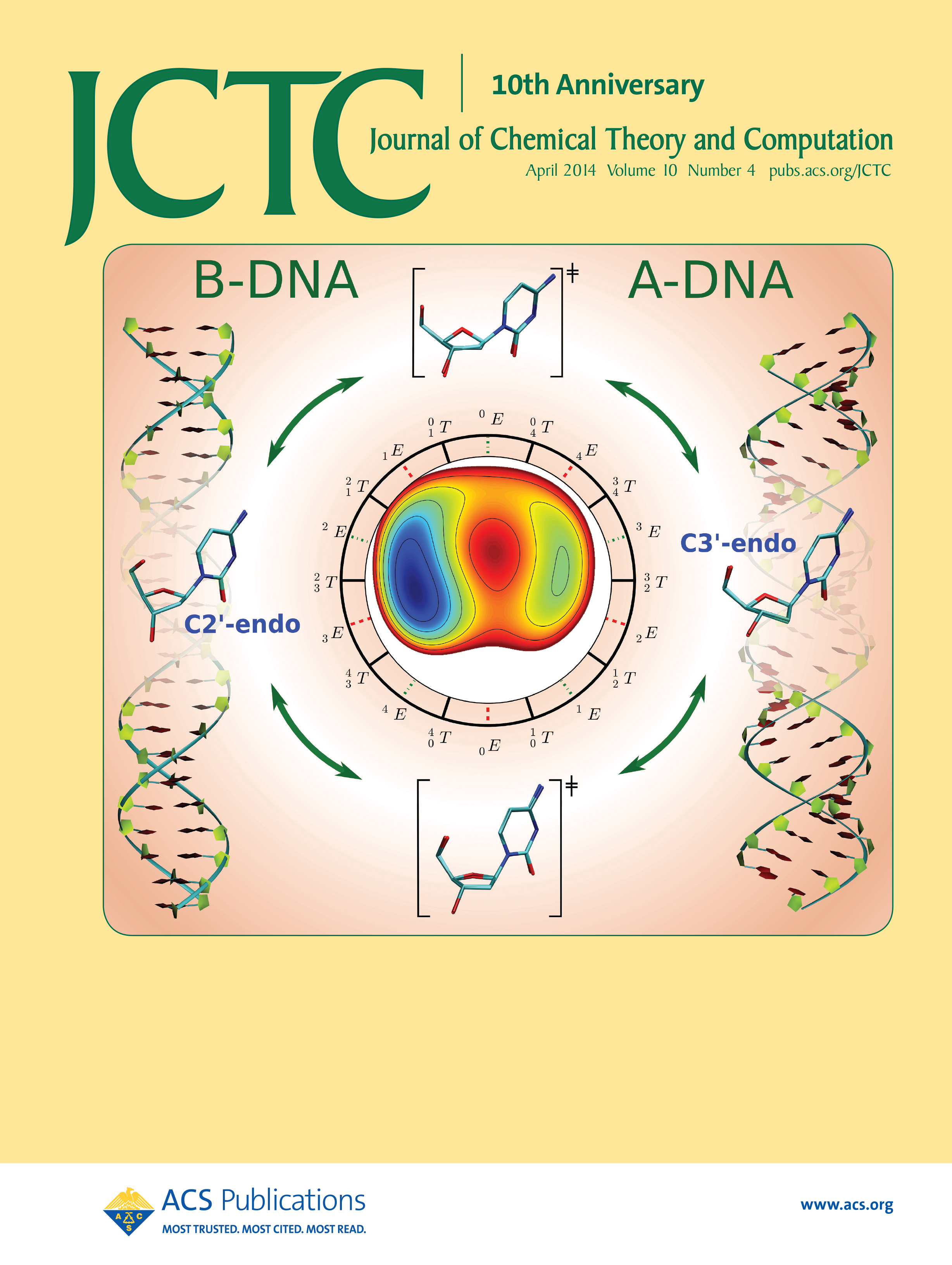
 | Yujun and Jinzhe's paper featured on the cover of JCTC! |
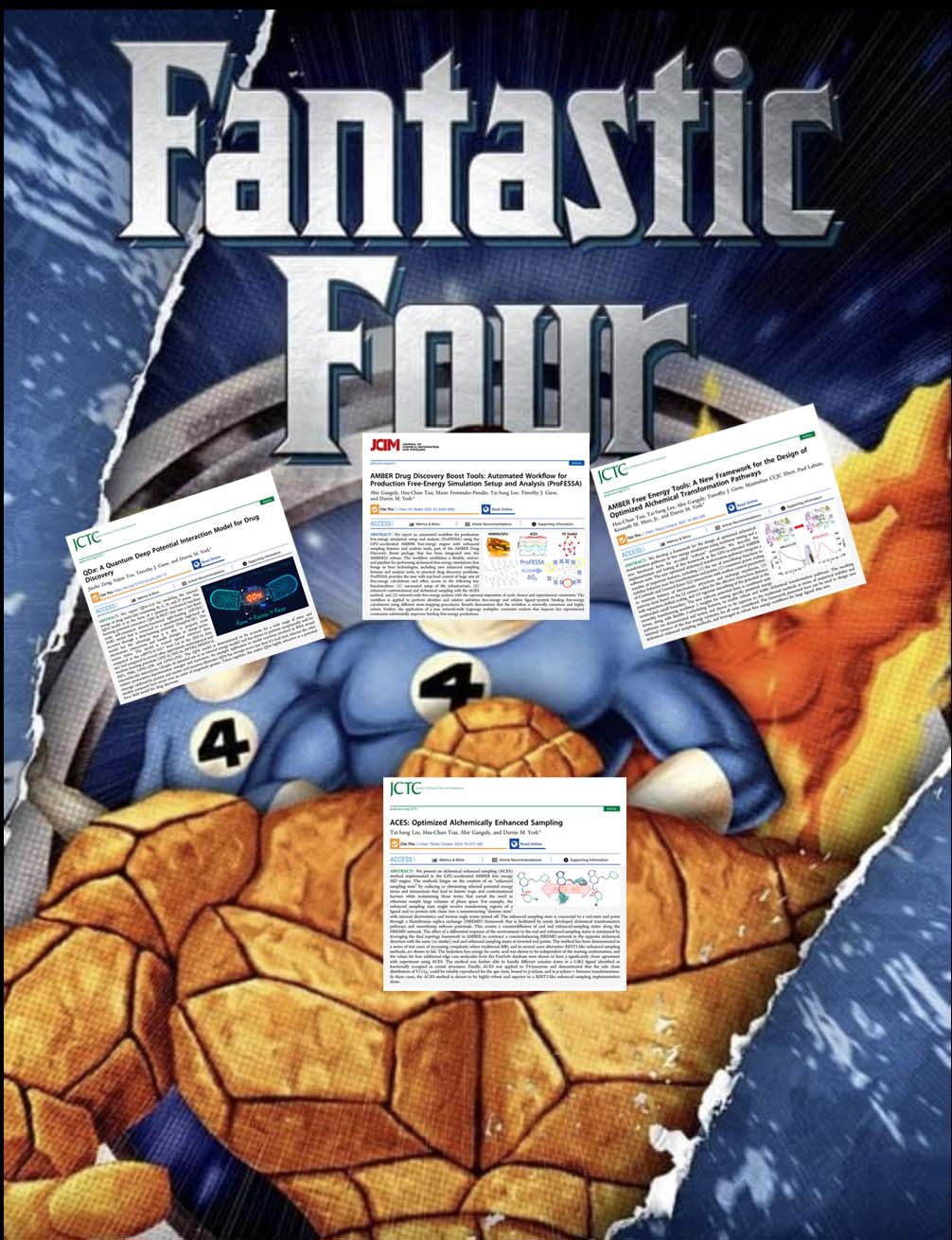 | YorkLab set of "fantastic 4" drug discovery papers just out! |
 | Jinzhe won 2022-2023 Van Dyke Award for excellence in research! |
 | York Group graduate students meet Nobel Laureate Frances Arnold! |
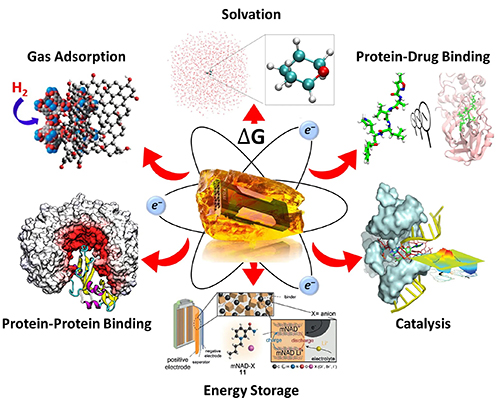 | York Lab shares NSF Cyberinfrastructure for Sustained Scientific Innovation (CSSI)! |
 | Shi got married! Congratulations to Shi & Jaiqi |
 | Şölen's best article EVER makes the JPC B cover! |
 | Hsu-Chun and Yujun win Reid and van Dyke awards for excellence in research |
 | York group book chapter on AMBER drug discovery boost is published! |
 | Jinzhe's first paper with the York Lab is out in JCTC! |
 | Ken successfully defended his thesis and survived pistols and hammerheads! Congratulations! |
 | Tim and Şölen's new paper is featured as the cover of JPC A! |
 | Tim's new paper solves all your relative binding free energies at once! |
 | Hsu receives the Van Dyke Research Award! |
 | Emily has a new paper out! |
 | Colin successfully defended his thesis, congratulations! |
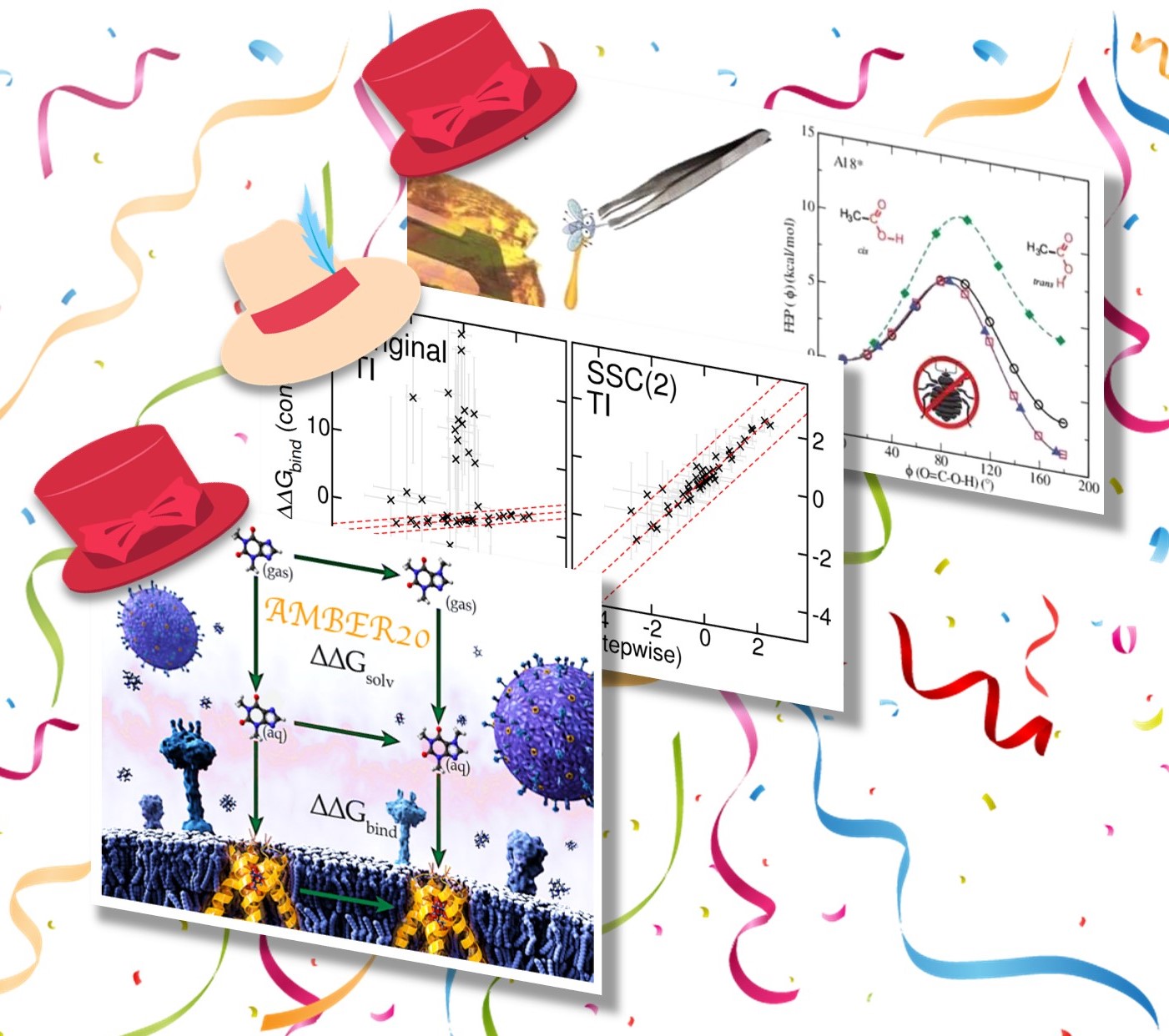 | York Lab "Hat-Trick" of new free energy papers published! |
 | Emily is Ph.inisheD. after a successful thesis defense! Congratulations! |
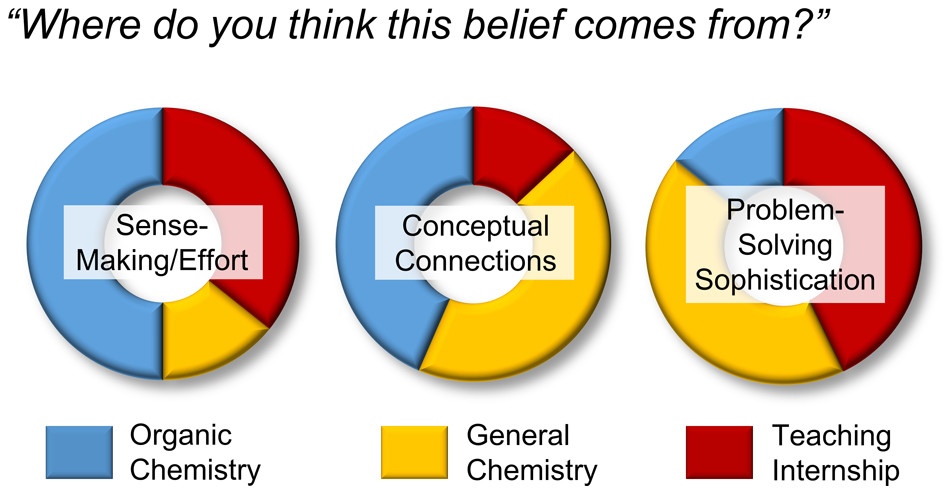 | Emily's paper on Peer Leader Learning Attitudes published in J. Chem. Ed.! |
 | York Lab awarded intramural research grant from the Center for COVID-19 Response and Pandemic Preparedness (CCRP2) |
 | Darrin is the recipient of the second annual Grossman Innovation Prize |
 | York lab among first cohort of researchers to gain access to the fastest academic supercomputer in the world |
 | Abir's paper on VS ribozyme published in Nature Chemistry! |
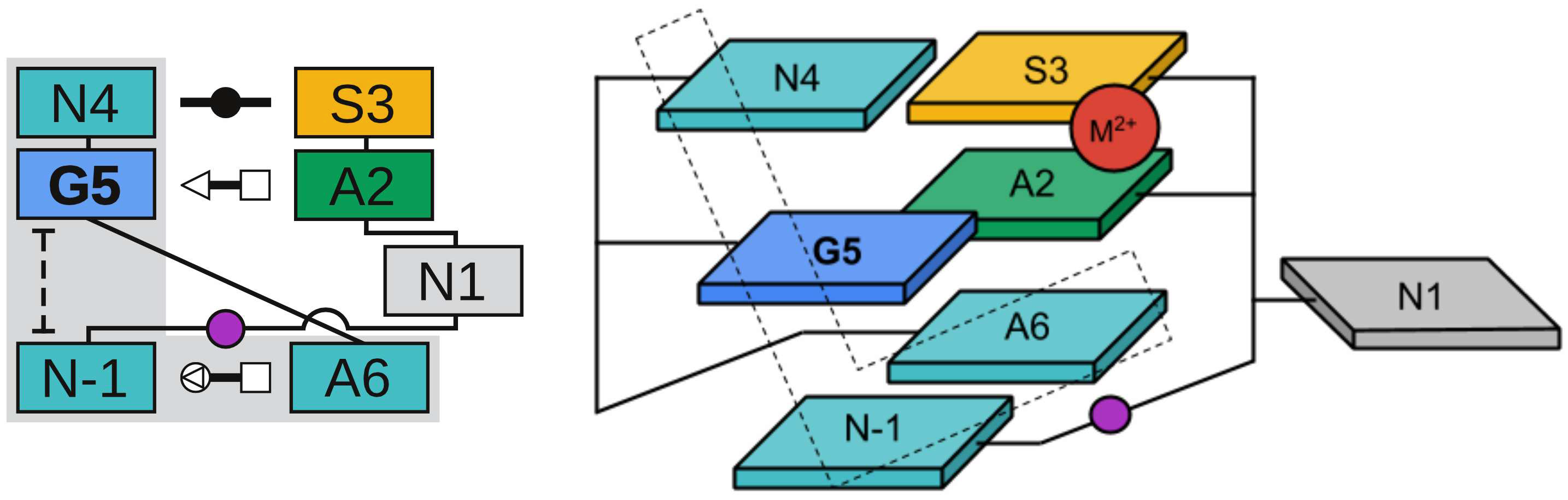 | Colin's paper on RNA enzyme design published in RNA! |
 | Yujun and Hsu pass their OFRP... Congratulations! |
 | Abir's paper has been selected as an ACS Editor's Choice article |
 | Darrin organizes an ACS symposium on integrating theory and experiment |
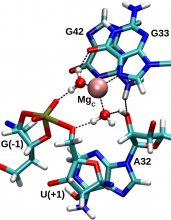 | Ken's Paper On The Pistol Ribozyme Accepted |
 | Şölen's crystal paper featured on cover of J. Phys. Chem. B |
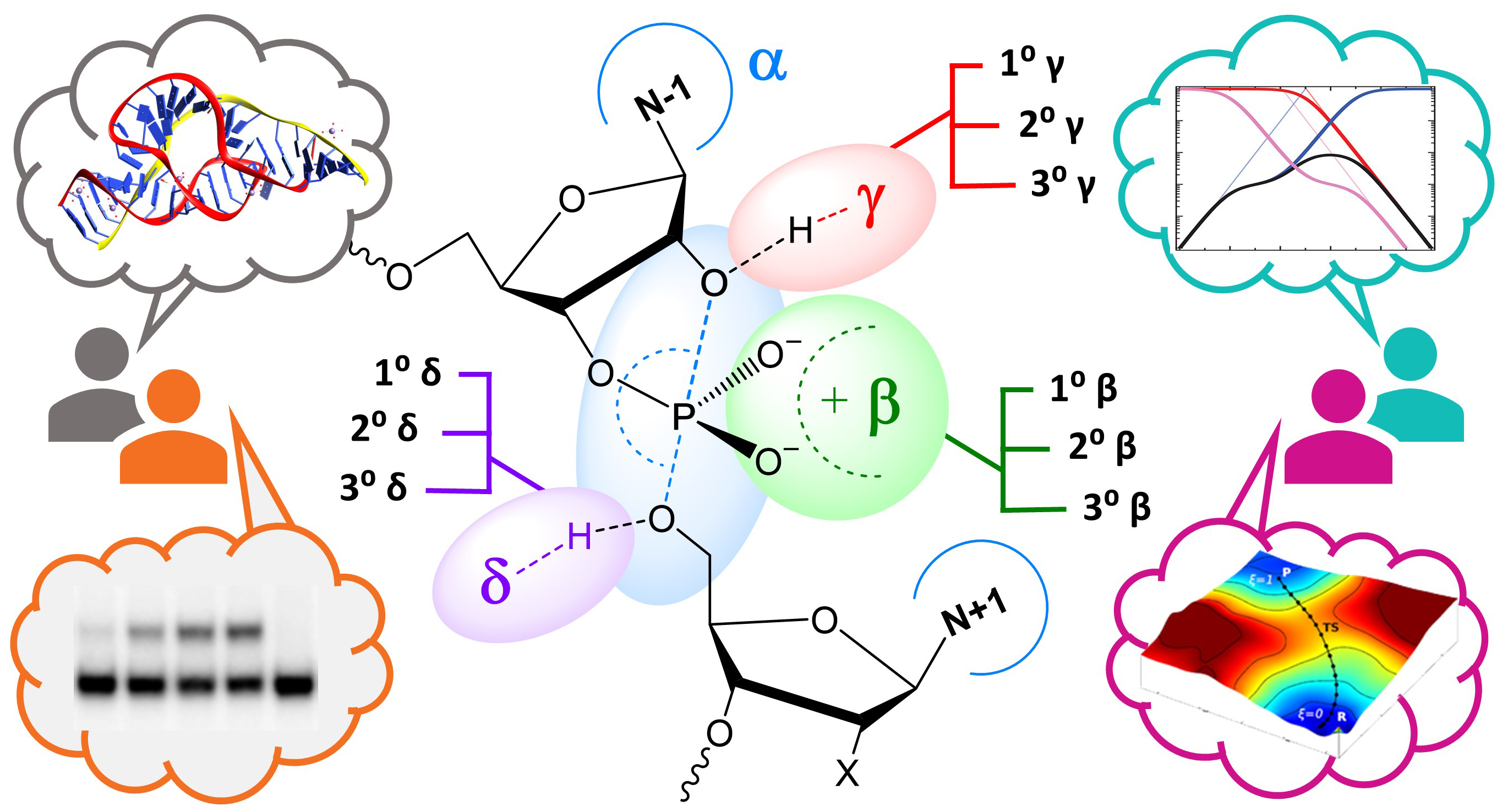 | York group leads new Ontology for discussion of RNA-cleavage reactions in ACS Chem. Biol. |
 | Şölen selected to receive "Promise in COMP" award |
 | Colin Wins Poster Award at Nucleic Acids Conference |
 | York Group at the Nucleic Acids Conference! |
 | George's JACS paper on Molecular Solvation Theory is now available! |
_0.jpg) | Emily Wins Rieman Award for Excellence in Teaching |
 | Ken Selected to Receive BASF Corporation Catalysts Division Fellowship |
 | Abir wins Best Poster at the Rutgers Postdoctoral Symposium! |
 | York Group Takes Retreat in Florida Following ACS Meeting |
 | LBSR Makes a Big Impact at the 255th ACS Meeting in New Orleans |
 | New GPU-accelerated free energy method in JCTC |
 | Ken and Emily Win Van Dyke Award for Excellence in Research |
 | Colin wins Reid Award for Outstanding Accomplishments in Doctoral Research |
 | Emily Atieh Publishes Book Chapter in ACS Symposium Series |
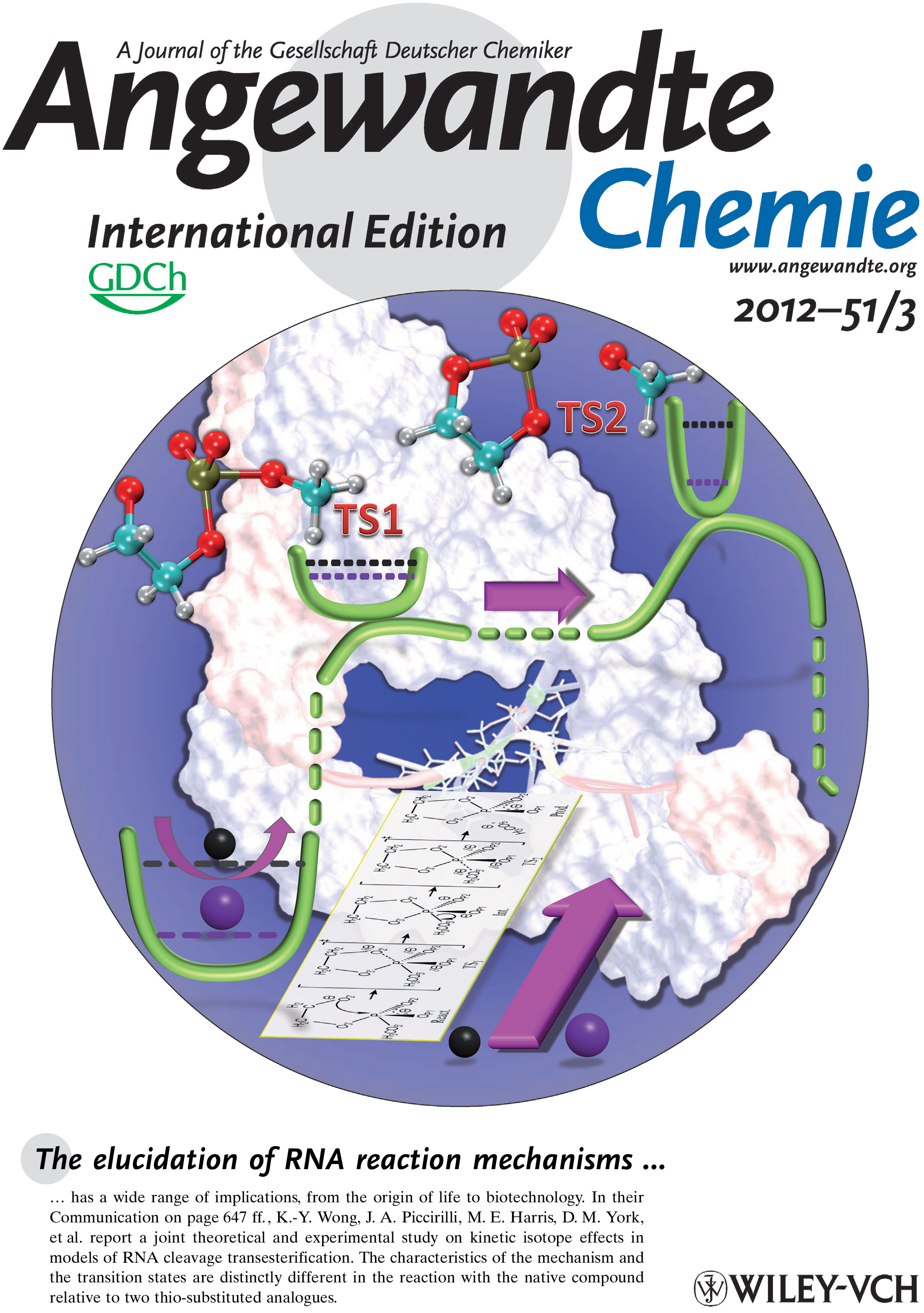
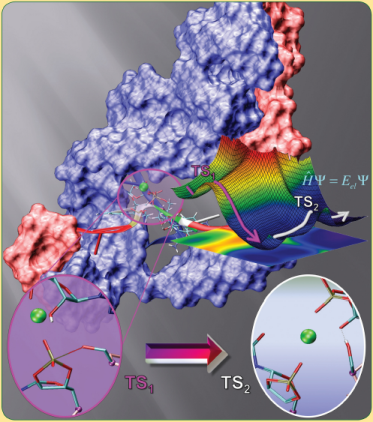
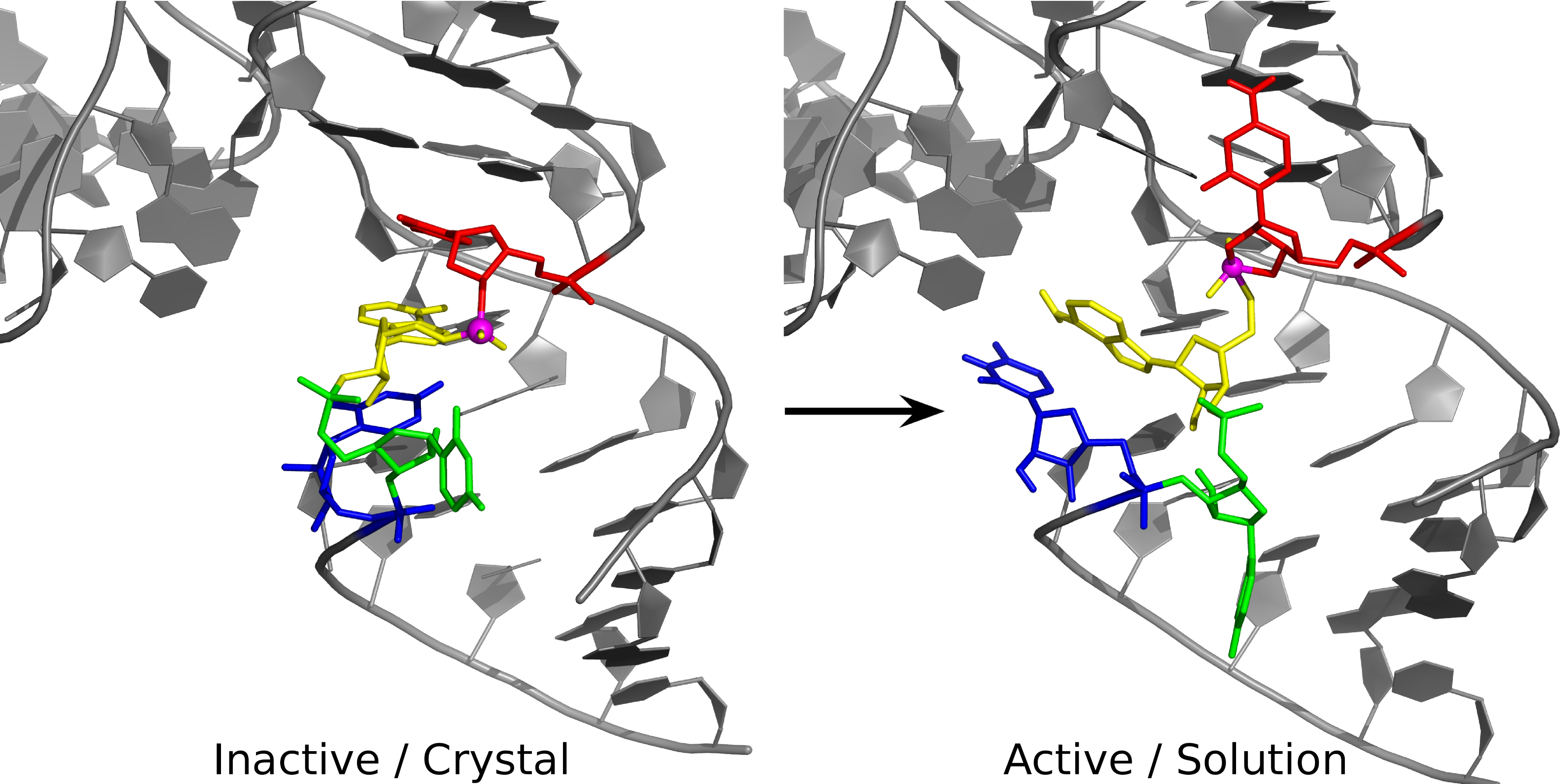 | Colin Gaines has paper accepted into Angewandte Chemie |
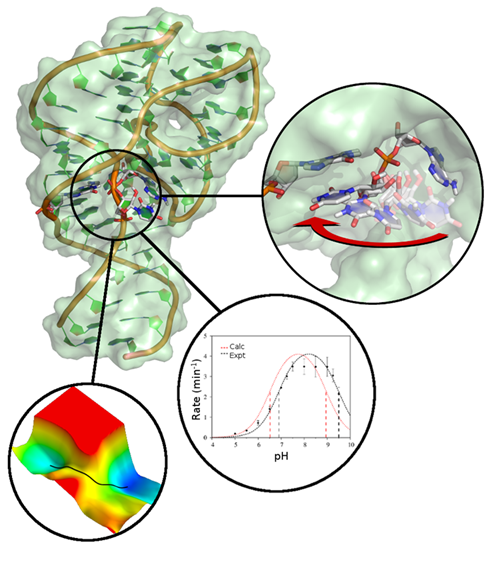 | Darrin York to give Closing Plenary Talk at QM/MM Methods and Applications conference At University of Manchester |
 | Darrin York attends CHARMM Developers Meeting at Harvard University |
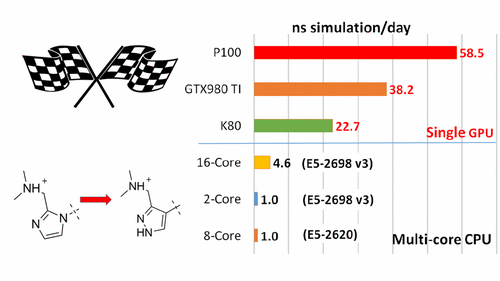 | New GPU-accelerated pmemdGTI module offers over 2 orders of magnitude speedup in free energy calculations |
 | Emily Atieh Presents at the Chemistry Education Research Conference at Miami University |
 | Darrin York Gives Opening Plenary Lecture at TheoBio17 in San Sebastian, Spain |
 | Ken Kostenbader Wins Duff Travel Award |
 | Emily Atieh attends AAAS-CASE Workshop in Washington D.C. |
 | Colin Gaines wins Van Dyke Award for Excellence in Research |
 | Emily Atieh Awarded Duff Travel Award |
 | 5th Zing Nucleic Acids Conference |
 | Darrin York Transforms Teaching in Active Learning Classrooms |
 | Darrin York's Attendance at Solvay Conference in Brussels |
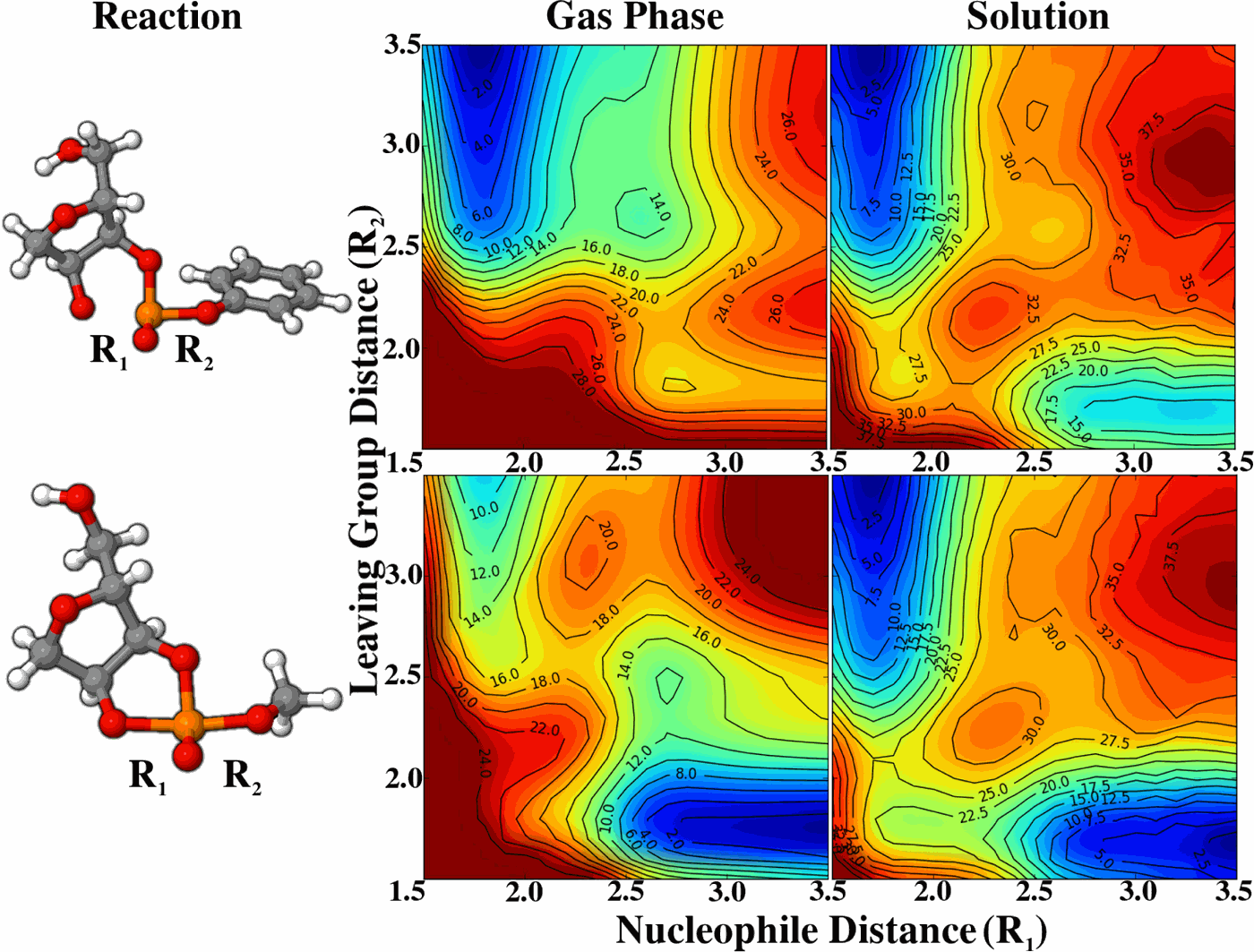 | JCP Editor's Pick |
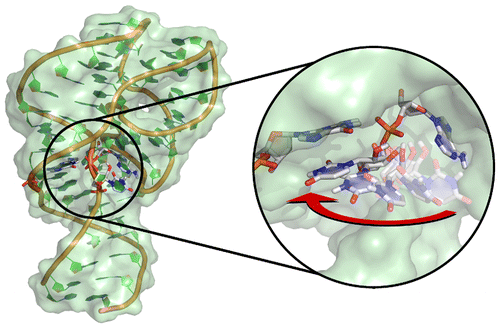 | Colin's Paper on Twister Ribozyme Featured in C&EN |
 | Haoyuan Chen Receives Reid Award for Outstanding Accomplishments in Doctoral Research |
 | Maria Panteva Successfully Defends Thesis! |
 | Erich Kuechler Successfully Defends Thesis! |
 | Thakshila Dissanayake Successfully Defends Thesis! |
 | Darrin York Named New Jersey Professor of the Year! |
 | Brian Radak Successfully Defends Thesis! |
 | Ming Huang Successfully Defends Thesis! |
 | Faculty Honored for Teaching, Research, Service, and Diversity Initiatives |
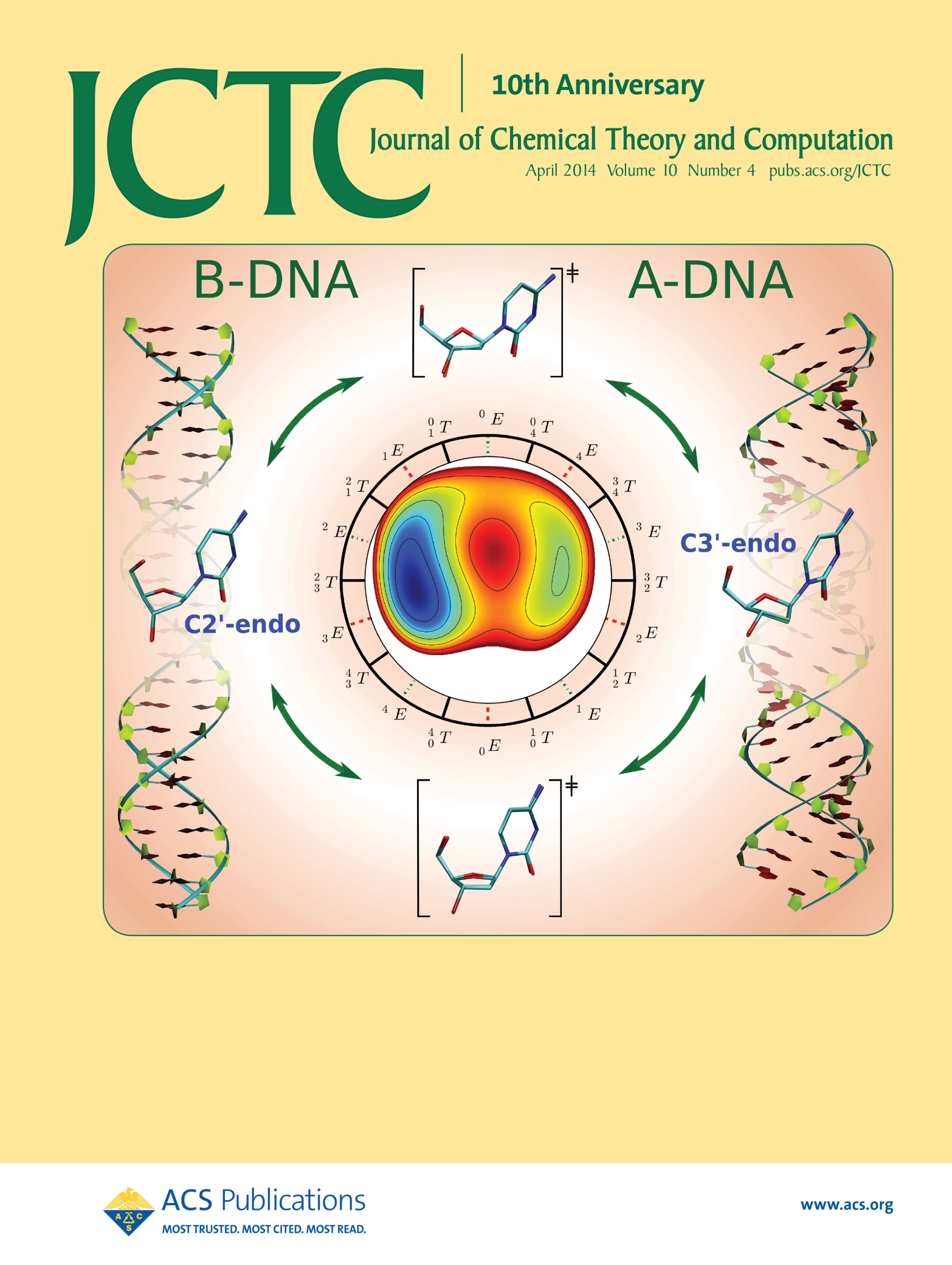 | Ming's Sugar Pucker Profile Paper Featured on April Cover of JCTC! |
 | Major Changes to Rutgers General Chemistry Course - First Page Headlines! |
 | High Achiever Recognition Ceremony |
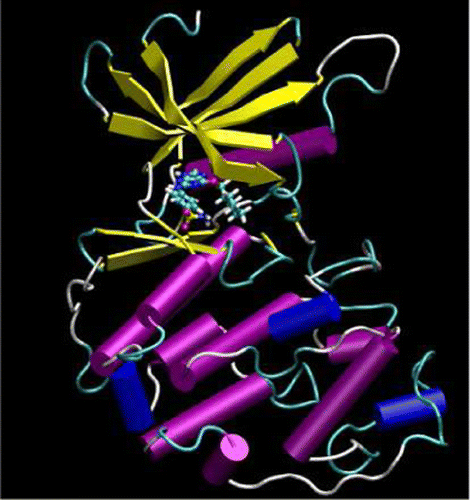 | Publication: "Parametrization of an Orbital-Based Linear-Scaling Quantum Force Field for Noncovalent Interactions" |
 | Darrin York's Talk at the Gordon Research Conference |
 | Bringing the "Wow" Factor to Chemistry Class |
 | Nobel Prize Winner Martin Karplus was Advisor to Three CCB Faculty |
 | 20 Years of PME: Symposium Honoring Professor Darrin York, Tom Darden, and Lee G Pedersen |
 | Professor Darrin York honored with SAS Award for Distinguished Contribution to Undergraduate Education |
 | Introducing a Novel E-Learning System Targeting Better Education for Students in the Science Industries |
 | Reaction Path and Transition States for RNA Transphosphorylation Models |
 | Molecules of RNA Form Biological Catalysts |
About Us
The York Lab develops innovative technology for advanced simulations of complex biological processes. We are co-developers of the Amber software package, and leaders in the field of computational drug discovery and nucleic acid enzyme design. Check out our team and recent papers!
Join Us
The York Lab is actively recruiting talented scientists to join our team. If you are a prospective graduate student, check out our Research (download brochure) and apply now to our graduate program in Chemistry & Chemical Biology or Quantitative Biomedicine. If you are interested in job opportunities as a postdoctoral fellow or research scientist, please contact Prof. York!
Contact
Mailing Address:
Center for Integrative Proteomics Research
174 Frelinghuysen Road
Piscataway, NJ 08854-8076